
When students learn the basic addition and subtraction facts for the first time, these simple relationships are “problems” for them to solve. In other words, they need to learn some means of arriving at the correct answer.
One of the findings from math education research is that an effective way to improve students’ ability to learn these basic addition and subtraction facts for the first time is to teach them systematic strategies for arriving at the answer when first learning the facts.
So the question becomes: If we’re going to teach strategies as a means to facilitate memorization, which strategies should we teach?
Learning the Basic Math Facts: Tens Complement vs. Doubles
In an earlier post, The 2 for 1 Special in Math: Basic Facts and Place Value Together, I described the tens complement approach to learning the basic addition and subtraction facts with sums or minuends greater than 10, along with some of the many benefits of that approach.
This strategy is used as the basis for teaching addition and subtraction in many East Asian countries – the same countries whose students have consistently scored the highest on international math assessments such as TIMMS. These same students are already well ahead of American students by the end of first grade, due in large part to their advantage in learning the basic addition and subtraction facts. Still, the tens complement approach is virtually non-existent in U.S. math education.
The primary approach used in the U.S. is simple rote repetition, as exemplified by the use of “flash cards.”
Over the past 30 years or so, many have advocated that students develop and use strategies for solving these problems. Unfortunately, far too much emphasis has been placed on 1) having students develop and use their own “invented” strategies and/or 2) using these strategies as a reason not to develop true fluency with the facts. There is yet a third reason to be concerned about this focus – the wrong strategy is usually advocated.
When a systematic strategy is advocated, it’s too frequently what is referred to as a “doubles” strategy, or “doubles-related” strategy, because the general strategy also includes the use of what are sometimes referred to as “near-doubles” facts. Below, I’ll use the term “doubles” strategy for both of these.
Addition Facts: Doubles Strategy
While this is referred to as a “strategy” its foundation lies in something that is not a strategy at all. It’s based on the fact that the “doubles” facts are the easiest to learn through repetition alone.
The “doubles” include these facts: 1 + 1, 2 + 2, 3 + 3, 4 + 4, 5 + 5, 6 + 6, 7 + 7, 8 + 8, and 9 + 9.
In order to use the “doubles” strategy, you must first memorize the doubles facts – and that’s almost always done using rote memorization.
The ease of learning these facts is likely related to the fact that learning them requires associating two numbers rather than three. For example, learning that 2 + 2 = 4 requires associating two numbers, 2 and 4. Learning that 2 + 3 = 5, on the other hand requires associating all three numbers, 2, 3, and 5.
The doubles strategy is based on the doubles facts. There are two associated strategies:
Doubles + 1
Doubles + 2
The doubles + 1 strategy applies to situations such as 4 + 5. The “double” in this case is 4 + 4. The 5 in 4 + 5 is 1 more than 4, so the sum is 1 more than 8, or 9, so 4 + 5 = 9.
The doubles + 2 strategy applies to situations such as 4 + 6. The 6 is 2 more than 4, so the sum is 2 more than 8, or 10, so 4 + 6 = 10.
Addition Facts: Tens Complement Approach
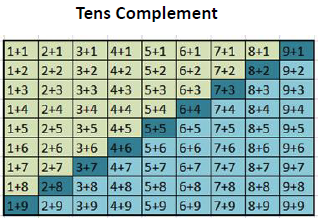
The tens complement strategy is based on the use of “tens complements.” The tens complements are two numbers that add to ten. These include 1 + 9, 2 + 8, 3 + 7, 4 + 6, 5 + 5, and the first four of these in reverse order.
These facts are the basis for the tens complement strategy that can be used to find the sum of any pair of single digit numbers whose sum is greater than 10.
The tens complement approach and how it works is covered in more detail in an earlier paper: The 2 for 1 Special in Math: Basic Facts and Place Value Together.
At iLearn, we call the tens complement approach “TenPals™.” The basis for the approach is the process of “making a ten” using knowledge of tens complements. The strategy for every fact, (whether addition or subtraction) is based on making a ten.
For example, to add 7 + 5, you first add 3 to 7, because 3 is the tens complement of 7.
Next, you add the “leftover” amount, which is 2, to 10.
The addition then becomes 7 + 3 + 2. Seven plus 3 is 10, and 10 plus 2 is 12. (Both of the latter facts should be taught to fluency before starting instruction on facts such as 7 + 5 using the tens complement strategy.)
With addition, you only need to learn and use tens complements for the digits 6 through 9. The reason is that any fact can be rearranged so that you always start with the larger number, so you will always start with the numbers 6 through 9. For example, the fact 3 + 8 = __ can be mentally re-ordered as 8 + 3 = __.
As a bonus, students learn from this that numbers can be added in any order, which is the “commutative property,” a very important concept in early numeracy/number sense. (This is not the case with subtraction, which will be addressed below.)
Comparison of Doubles and Tens Complement
The first comparison is in terms of the number of facts they can be used with.
The matrix below shows the 81 addition facts for digits 1-9.
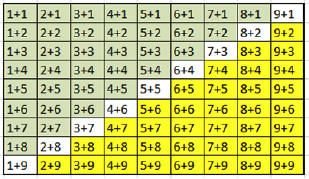
The facts highlighted in green are the facts with sums less than 10. These 36 facts are the easiest for students to learn.
The facts highlighted in yellow are the facts with sums greater than 10. These 36 facts are the most difficult to learn, and the ones most deserving attention.
The remaining 9 facts are those whose sum equals 10. These are the “tens complement” facts.
The illustrations below show which of the difficult facts can be learned using the doubles strategy on the left and the tens complement strategy on the right.
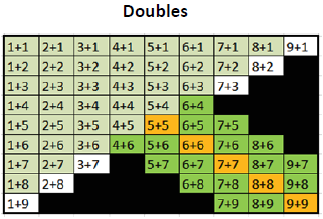
In the illustration on the left, the difficult doubles facts are highlighted in orange. As noted above, there is no strategy associated with learning the 5 doubles facts. Students just learn them on their own through repetitive practice (e.g., rote memorization, visual recognition, etc.).
The 16 doubles-related facts are shown in darker green in the illustration on the left. Of these, 14 apply to the most difficult facts and the remaining 2 apply to facts with a sum of 10 (4 + 6 and 6 + 4).
For the remaining 18 facts shown in black, there is no doubles strategy. Neither the double + 1 nor the double + 2 strategy applies because the difference in the two numbers being added is 3 or more in each case.
Advocates of the “doubles” strategies typically point out that these 18 facts can be learned with other strategies usually described as being “related to the number 10,” but these strategies are typically not spelled out in detail. In reality, they are referring to the Tens Complement approach described here.
In summary, the doubles strategy can be helpful in less than half of the difficult addition facts. There are 14 facts where it is helpful and 18 facts where it is not.
One of the major benefits of the tens complement approach, on the other hand, is that a single strategy can be used for a larger number of facts.
More importantly, these facts are the very facts that are the most difficult to learn.
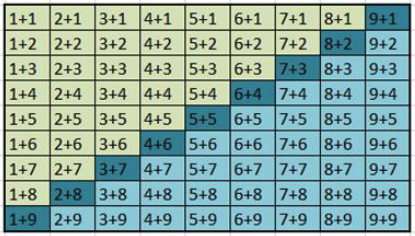
The matrix above shows the facts that can be taught with this strategy.
The 9 facts highlighted in dark blue are the facts that have a sum of 10. These are the “tens complements.”
The 36 facts in lighter blue are the addition facts that can be solved using the tens complement approach.
What is most significant about these 36 facts is that they are all of the addition facts that are most difficult for students to learn.
Here’s a summary of the benefits of the two for the 36 most difficult addition facts:

The doubles strategy can be used with 14 of the most difficult addition facts.
The tens complement approach can be used with all 36 of the most difficult addition facts.
This, in itself, is a clear advantage for the tens complement approach.
But that’s only half the story. The other half is about subtraction.
Subtraction Facts: Doubles Strategy
It’s rare to hear anyone discuss the use of any strategies for teaching the basic subtraction facts, including doubles strategies. That’s unfortunate in light of the fact that most students have more difficulty learning the subtraction facts than the addition facts.
You might think that it would also be helpful to use the doubles strategy with subtraction, but that’s not the case.
With addition, it’s easy to see when the doubles strategy is useful. There is always a larger and a smaller number. In some cases, the difference in the two numbers is 1 and some cases it’s 2.
So the steps needed to apply the doubles strategy is the same in each case:
With subtraction, it’s not as simple.
For example, with addition, the two facts below use the same numbers, and both can both be solved by a doubles + 1 strategy in the same way:
7 + 8
8 + 7
In either case, you double the smaller number, 7, and add 1.
For the comparable subtraction facts, the situation is much more complex. When these two facts are converted to subtraction you have these two facts:
15 – 7
15 – 8
Most people would assume that you start by doubling the single digit in each case, but that’s not correct. That’s the first difficulty with this approach.
That means it’s not obvious in any problem whether the doubles strategy applies, and, if so, what number to double. This results in multiple rules to handle the 14 facts related to the addition facts identified above. Also, remember that “taking half” of a number has no meaning for students at this level, so that can’t be used as part of the strategy.
Based on these facts, it’s clear that the doubles strategy provides little or no benefit for learning the subtraction facts.
If you feel this conclusion is not justified, try using the near-doubles strategy to solve these problems.
Was it easy? Was the strategy helpful?
Probably not. And, if it was hard for you, think about how difficult it would be for a first grader attempting it.
There’s good news, however. There is a far better approach for subtraction facts. Again, it’s the tens complement approach.
Subtraction Facts: The tens complement approach
The tens complement approach is based on the “missing addend” definition of subtraction. (For an explanation of the “missing addend” definition, see What is Subtraction?). In fact, the “complement” of a number is the same thing as a “missing addend.”
Subtraction is also based on first “making a ten,” which is the simple application of the basic principle of place value. (For more on this, see: The 2 for 1 Special in Math: Basic Facts and Place Value Together.)
Here’s an example of the tens complement approach. We’ll subtract 7 from 12.

We can easily see that what we need to find is the number we add to 7 to get 12. That’s the “missing addend” definition of subtraction.
We find the missing addend in two steps. The first is to find the number we need to add to 7 to get 10.
That’s the tens complement of, 7, which is 3, since 7 + 3 = 10.

You then need to add a number to 10 to make 12. That number is 2 because 10 + 2 = 12, and students have already learned to fill in the missing addend in this statement: 10 + __ = 12.

At this point, we’ve used two facts the students already know:
7 + 3 = 10
10 + 2 = 12
The last step is to use another fact that students already know. You add 3 and 2 to get 5.

To recap, you started with 7, then added 3 more to make a ten, then added 2 to get 12. Last, you added 3 and 2 to get 5. So the number you add to 7 to get 12 is 5. That means the difference in 12 and 7 (12 – 7) also equals 5.
So, to complete the subtraction, the student is only required to use a simple strategy along with 3 facts they already know.
And, as a bonus, the three facts required to do this are all addition facts, even though this is a subtraction problem. That makes the task even easier, since addition facts are much easier for most students to learn and remember.
Over time, students learn to immediately see the tens complement 3 (which makes a 10) and another 2 to make 12 as the numbers needed to complete the addition. And, just as easily, they see that 3 and 2 make 5, so the difference is 5. For more on this, see The 2 for 1 Special in Math: Basic Facts and Place Value Together.
The tens complement approach works equally well for both subtraction and addition, and is just as easy for subtraction as it is for addition. And, as was the case for addition, it can also be used with all 36 of the most difficult subtraction facts.
Here’s a summary of the benefits of the two strategies for addition and subtraction.
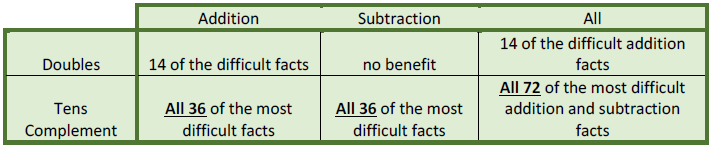
The doubles strategy can be used with only 14 of the addition facts, and is not useful for subtraction.
Again, on the basis of these benefits alone, the tens complement approach is superior to the doubles strategy for learning the subtraction facts.
When we put the addition and subtraction facts together, as in the last column, the benefits of the tens complement approach clearly outweigh those of the doubles strategy.
The doubles strategy is beneficial for only 14 of the most difficult addition facts and no subtraction facts.
The tens complement approach is beneficial for all 72 of the most difficult facts, including all difficult addition and all difficult subtraction facts.
These benefits in learning the facts can be described as benefits in ease of learning. They make it far easier to develop both accuracy and fluency in learning the basic facts.
But as noted in an earlier paper (The 2 for 1 Special in Math: Basic Facts and Place Value Together), there is another huge benefit from this approach. It teaches the basic principle of place value starting with the sums and difference of single digits, rather than having it introduced later with sums and differences of two-digit numbers.
Given these exceptional benefits, it’s difficult to understand why the doubles strategy has received far more attention and support than the tens complement approach in American math education.
You be the judge.
Click below for other Resources